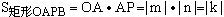課程內容
第26章《反比例函數》26.1.2 反比例函數的圖象與性質(2)
填表分析正比例函數和反比例函數的區別
| 函數 |
正比例函數 |
反比例函數 |
| 解析式 |
y=kx(k≠0) |
y=k/x(k是常數,k≠0) |
| 圖象形狀 |
直線 |
雙曲線 |
| k>0 |
位置 |
一三象限 |
一三象限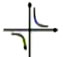 |
| 增減性 |
y隨x的增大而增大 |
y隨x的增大而減小 |
| k<0 |
位置 |
二四象限 |
二四象限 |
| 增減性 |
y隨x的增大而減小 |
y隨x的增大而增大 |
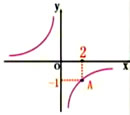
(1)這個函數的圖象分布在哪些象限?y隨x的增大如何變化?
(2)點B(3,4)、C(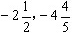 )和D(2,5)是否在這個函數的圖象上?
)和D(2,5)是否在這個函數的圖象上?
解:(1)設這個反比例函數為y=k/x,
∵圖象過點A(2,6)
∴6=k/2 解得:k=12
∴這個反比例函數的表達式為y=12/x
∵k>0
∴這個函數的圖象在第一、第三象限,在每個象限內,y隨x的增大而減小。
(2)把點B、C和D的坐標代入y=12/x,可知點B、點C的坐標滿足函數關系式,點D的坐標不滿足函數關系式,所以點B、點C在函數y=12/x的圖象上,點D不在這個函數圖象上。
練習
1、反比例函數的圖象如圖所示,則其解析式為________。
2、下列各點在雙曲線y=-2/x上的是( )
A、(-4/3,-3/2) B、(-4/3,3/2)
C、(3/4,-4/3) D、(3/4,8/3)
3、反比例函數y=k/x的圖象經過點(2,5),若點(1,n)在反比例函數圖象上,則n等于( )
A、10 B、5 C、2 D、-6
例2:如圖是反比例函數y=(m-5)/x的圖象一支,根據圖象回答下列問題:
(1)圖象的另一支在哪個象限?常數m的取值范圍是什么?
(2)在這個函數圖象的某一支上任取點A(a,b)和B(a',b'),如果a>a',那么b和b'有怎樣的大小關系?
解:(1)反比例函數圖象的分布只有兩種可能,分布在第一、第三象限,或者分布在第二、第四象限。這個函數的圖象的一支在第一象限,則另一支必在第三象限。
∵函數的圖象在第一、第三象限
∴m-5>0
解得m>5
(2)∵m-5>0,在這個函數圖象的任一支上,y隨x的增大而減小
∴當a>a'時,b<b'
練習
1、已知點A(-2,y1),B(-1,y2)都在反比例函數y=k/x(k>0)的圖象上,則y1與y2的大小關系為______。
2、已知點A(x1,y1),B(x2,y2)且x1<0<x2都在反比例函數y=k/x(k<0)的圖象上,則y1與y2的大小關系(從大到小)為______。
3、在反比例函數y=(a2+1)/x的圖象上有三點(x1,y1)、(x2,y2)、(x3,y3),若x1>x2>0>x3,則下列各式中正確的是( )
A、y3>y1>y2 B、y3>y2>y1
C、y1>y2>y3 D、y1>y3>y2
面積性質(一)
設P(m,n)是雙曲線y=k/x(k≠0)上任意一點,有:
(1)過P作x軸的垂線,垂足為A,則
面積性質(二)
(2)過P分別作x軸,y軸的垂線,垂足分別為A、B,則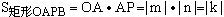
思維訓練一
1、如圖,點p是反比例函數圖象上的一點,過點P分別向x軸、y軸作垂線,若陰影部分面積為3,則這個反比例函數的關系式______。
2、一個反比例函數在第三象限如圖所示,若A是圖象上任意一點,AM⊥y軸于M,O是原點,如果△AOM的面積是3,那么這個反比例函數的解析式是什么?
3、如圖,A、C是函救y=1/x的圖象上任意兩點,過A作x軸的垂線,垂足為B,過C作y軸的垂線,垂足為D。若Rt△AOB的面積為S1,Rt△OCD的面積為S2,則______。
A、S1>S2
B、S1<S2
C、S1=S2
D、S1和S2的大小關系不能確定
4、如圖,在y=1/x(x>0)的圖象上有三點A,B,C,經過三點分別向x軸引垂線,交x軸于A1,B1,C1三點,邊結OA,OB,OC,記△OAA1,△OBB1,△OCC1的面積分別為S1,S2,S3,則有______。
A、S1=S2=S3
B、S1<S2<S3
C、S3<S1<S2
D、S1>S2>S3
5、如圖,點A、B在反比例函數y=k/x(k>0,x>0)的圖象上,過點A,B做x軸的垂線,垂足分別為M,N,延長線段AB交x軸于點C,若OM=MN=NC,△AOC的面積為6,則k的值為______。
思維訓練二
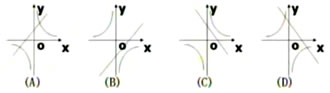
1、若ab<0,則函數y=ax與y=b/x在同一平面直角坐標系中的圖象大致是( )
2、函數y=kx-k與y=k/x(k≠0)在同一條直角坐標系中的圖象可能是_____。
3、設x為一切實數,在下列函數中,當x減小時,y的值總是增大的函數是( )
A、y=-5x-1 B、y=x/2
C、y=-2x+2 D、y=4x
思維訓練三
如圖,已知反比例函數y=12/x的圖象與一次函數y=kx+4的圖象相交于P、Q兩點,且P點的縱坐標是6。
(1)求這個一次函數的解析式。
(2)求三角形POQ的滿級。
本課小結
通過本節課的學習,我們掌握了
1、能利用反比例函數的圖象和性質解決簡單的問題。
2、掌握“k”的幾何意義。
3、會求反比例函數圖象中的一些圖形的面積。




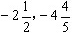 )和D(2,5)是否在這個函數的圖象上?
)和D(2,5)是否在這個函數的圖象上?